News
Die Veranstaltung "Numerische Methoden in der Elektrodynamik" findet im Sommersemster 2022 als Blockveranstaltung in Präsenz statt.
The course "Numerical Methods in Electrodynamics" will take place in the summer semester 2022 as a block course in presence.
- Titel: Numerische Methoden in der Elektrodynamik
- Datum: 5-9 September 2022, 8:00-16:00 Uhr
- Raum: Ruhr-Universität Bochum, ID 04/401
- Veranstaltungsart: Blockveranstaltung (Vorlesung mit integrierten Übungen)
- Kreditpunkte: 4
- SWS: 3
- Sprache: Deutsch
- Prüfung: mündliche Prüfung (ca. 30 min)
- Title: Numerical Methods in Electrodynamics
- Date: 5-9 September 2022, 8 am to 4 pm
- Room: Ruhr University Bochum, ID 04/401
- Event Type: Block course (lecture with integrated exercises)
- Credits: 4
- SWS: 3
- Language: German
- Exam: oral Exam (ca. 30 min)
Zusammenfassung
Summary
In diesem Kurs lernen die Studierenden die Grundlagen numerischer Methoden kennen, die insbesondere im Bereich der Elektrodynamik von zentraler Bedeutung sind. Nach einer kurzen Einführung in die Programmiersprache Python und die entsprechenden wissenschaftlichen Bibliotheken führen die Studierenden selbstständig numerische Berechnungen in verschiedenen Bereichen durch. Dazu gehören Feldberechnungen, die Simulation von Teilchenbewegungen, Interpolationsmethoden und die Lösung von partiellen Differentialgleichungen. Neben der numerischen Umsetzung der jeweiligen Methoden soll auch die Visualisierung der Ergebnisse im Vordergrund stehen.
In this course, students learn the basics of numerical methods, which are of central relevance especially in the field of electrodynamics. After a short introduction to the programming language Python and the corresponding scientific libraries, the students will independently perform numerical calculations in various fields. These include field calculations, simulation of particle motion, interpolation methods and solution of partial differential equations. In addition to the numerical implementation of the respective methods, the visualization of the results should also be in the focus.
Inhalt
Content
- Motivation
- Einführung Python
- Diskretisierung
- Finite Differenzen Methode (FDM)
- Explizite und implizite Verfahren
- Teilchenbewegung in elektrischen und magnetischen Feldern (Leap-Frog Verfahren und Boris-Pusher)
- Interpolationsverfahren
- Lösung der Poisson-Gleichung (elliptische DGL)
- Lösung der Diffusionsgleichung (parabolische DGL)
- Lösung der Wellengleichung (hyperbolische DGL)
- Ausblick Python und numerische Methoden
- Motivation
- Introduction Python
- Discretization
- Finite Differenzen Method (FDM)
- Explicit and implizit methods
- Particle motion in electric and magnetic fields (Leap-Frog Method and Boris-Pusher)
- Interpolation method
- Solution of Poisson's equation (elliptic PDE)
- Solution of diffusion equation (parabolic PDE)
- Solution of wave equation (hyperbolic PDE)
- Outlook Python and numerical methods
Feldberechnung
Field Calculation
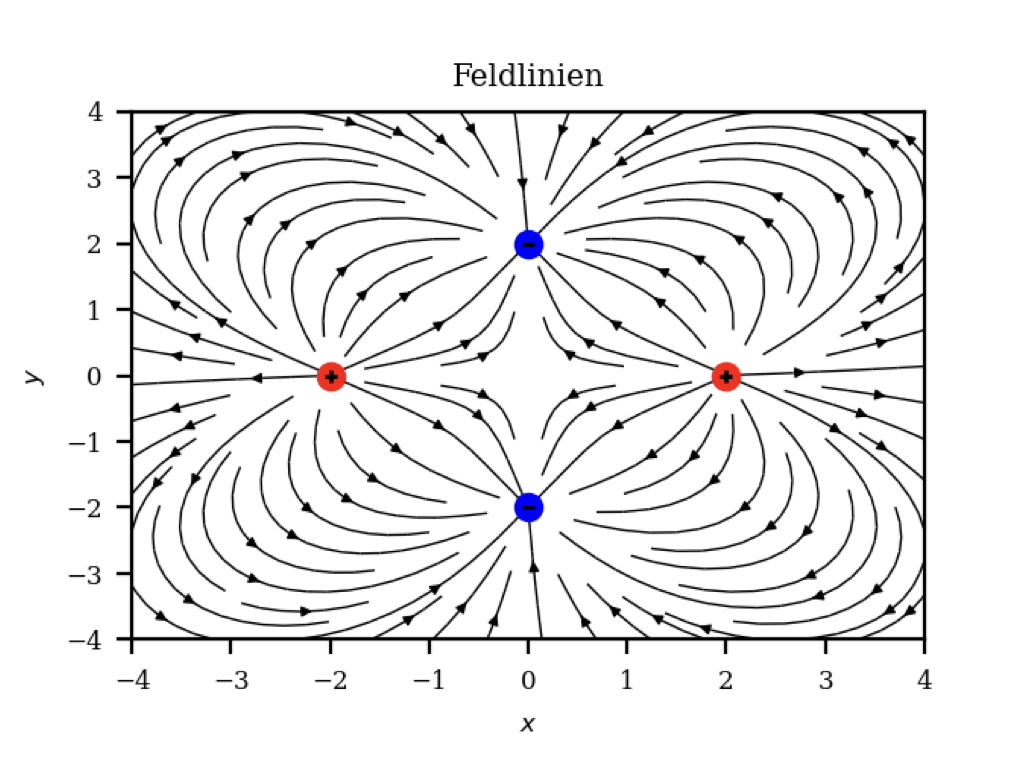
Aus der Elektrostatik ist bekannt, dass das elektrische Feld sehr einfach nach dem Coulobschen Gesetz bestimmt werden kann. Numerisch ist dies ebenso einfach zu lösen. Über einen Zufallszahlengenerator können geladene Teilchen zufällig in einem diskreten Gebiet verteilt werden, die resultierenden elektrischen Feldlinien werden über einen Streamplot visualisiert und das elektrische Potential kann in einem Contour-Plot dargestellt werden. Bei einer größeren Anzahl von geladenen Teilchen stößt der Rechner jedoch schnell an seine Grenzen, da die Wechselwirkung aller geladenen Teilchen untereinander berücksichtigt werden muss.
It is known from electrostatics that the electric field can be determined very easily according to Coulob's law. Numerically, this is just as easy to solve. Via a random number generator, charged particles can be randomly distributed in a discrete area, the resulting electric field lines are visualized via a stream plot and the electric potential can be displayed in a contour plot. However, with a larger number of charged particles, the computer quickly reaches its limits, since the interaction of all charged particles with each other must be taken into account.
Gewöhnliche Differentialgleichungen
Ordinary Differential Equations

In vielen Bereichen der Ingenieurwissenschaften oder der Physik spielen gewöhnliche und partielle Differentialgleichungen eine zentrale Rolle. Diese können mit der Finite-Differenzen-Methode (FDM) auf einer endlichen Anzahl von diskreten Stützstellen berechnet werden. Grundlegende Ein- und Mehrschrittverfahren, wie das Euler-Vorwärts- und Rückwärts-Verfahren, die Trapezregel oder andere Methoden aus der Familie der Runge-Kutter-Verfahren, werden vorgestellt und anhand von Beispielen numerisch umgesetzt. Die Vor- und Nachteile der Methoden sowie der Unterschied zwischen impliziten und expliziten Konzepten werden aufgezeigt.
In many areas of engineering or physics, ordinary and partial differential equations play a central role. These can be computed by the finite difference method (FDM) on a finite number of discrete grid points. Fundamental single-step and multi-step methods, such as the Euler forward and backward method, the trapezoidal rule or other methods from the family of Runge-Kutter methods, are introduced and numerically implemented by means of examples. The advantages and disadvantages of the methods as well as the difference between implicit and explicit concepts will be highlighted.
Bewegungsgleichung (instabil)
Equation of motion (unstable)
Eine besondere Herausfordung liegt in der numerischen Lösung der Bewegungsgleichung, welche in der klassischen Mechanik eine wichtige Rolle spielt. Die Geschwingkeit und der Ort sind durch zwei gewöhnliche Differentialgleichungen gekoppelt und werden numerisch integriert. Eine einfache Vorwärts-Differenzen-Methode ist von Natur aus jedoch instabil. Somit führt eine simple Oszillationsbewegung (z.B. eines Pendels oder einer Teilchenoszillation) zu einem divergierenden Ergebnis in Bezug auf die Position und die Geschwindigkeit.
A particular challenge is the numerical solution of the equation of motion, which plays an important role in classical mechanics. The velocity and the position are coupled by two ordinary differential equations and are integrated numerically. However, a simple forward difference method is inherently unstable. Thus, a simple oscillatory motion (e.g. of a pendulum or a particle oscillation) leads to a divergent result in terms of position and velocity.
Bewegungsgleichung (stabil)
Equation of motion (stable)
Um numerische Instabilitäten zu vermeiden, wird zur Lösung der Bewegungsgleichung die Leap-Frog-Methode genutzt. Mit dieser Methode wird abwechselnd die Position und die Geschwindigkeit zu unterschiedlichen Zeitpunkten berechnet. Unter Berücksichtigung von Stabilitätsbedigungen, welche speziell für explizite Verfahren vorgestellt werden, kann die Bewegung eines Objektes/Teilchens nahezu exakt numerisch berechnet werden.
In order to avoid numerical instabilities, the leap-frog method is used to solve the equation of motion. With this method, the position and the velocity are calculated alternately at different times. Considering stability conditions, which are presented especially for explicit methods, the motion of an object/particle can be calculated numerically.
Teilchenbewegung in magnetischen Feldern
Particle motion in magnetic fields
Um die Bewegung von geladenen Teilchen in elektrischen und magnetischen Feldern numerisch berechnen zu können, wird das Leap-Frog Verfahren mit dem sogennanten Boris-Puhser erweitert. So können typische Trajektorien in einem magnetischen Feld dargestellt werden.
Um die Bewegung geladener Teilchen in elektrischen und magnetischen Feldern numerisch zu berechnen, wird die Leap-Frog-Methode um den sogenannten Boris-Puhser erweitert. Damit können typische Trajektorien in einem Magnetfeld dargestellt werden.
ExB-Drift
ExB-Drift
Die erlernten Techniken können zur Simulation der Bewegung geladener Teilchen in verschiedenen Feldkonfigurationen verwendet werden. Wenn beispielsweise eine senkrechte Komponente zwischen der magnetischen und der elektrischen Feldkomponente existiert, wird das geladene Teilchen in eine Richtung abgelenkt, die sowohl zum magnetischen als auch zum elektrischen Feld senkrecht steht (ExB-Drift).
The techniques learned can be used to simulate the motion of charged particles in different field configurations. For example, if there is a perpendicular component between the magnetic and electric field components, the charged particle will be deflected in a direction perpendicular to both the magnetic and electric fields (ExB drift).
Prokekt: Simulation von geladenen Teilchen in einem Geschwindigkeitsfilter
Project: Simulation of charged particles in a velocity selector
Um die erlernten numerischen Methoden auf praktische Probleme anwenden zu können, sollen sich die Studierenden mit der Bewegung von geladenen Teilchen (Elektronen und Ionen) in einem Geschwindigkeitsfilter (Wien-Filter) auseinandersetzen. Sowohl die elektrische als auch die magnetische Feldstärke müssen geeignet gewählt werden, um die geladenen Teilchen mit einer bestimmten Geschwindigkeit herauszufiltern.
In order to apply the studied numerical methods to practical problems, the students have to deal with the motion of charged particles (electrons and ions) in a velocity selector (Wien filter). The electric as well as the magnetic field force must be chosen appropriately to filter out the charged particles with a certain velocity.
Poisson-Gleichung
Poisson's Equation
Im letzten Teil der Vorlesung werden numerische Konzepte für partielle Differentialgleichungen vorgestellt. Die 2D- und 3D-Poisson-Gleichung ist eine elliptische DGL, die die Beziehung zwischen elektrischem Potential und Raumladungsdichte beschreibt. Bei gegebenen Randbedingungen und vorhandener Ladungsdichteverteilung kann das Potential auf verschiedene Arten numerisch bestimmt werden. Die Gauß-Seidel-Methode ist ein iterativer Ansatz, der das räumlich aufgelöste Potential in einem linearen Gleichungssystem approximiert. Vor- und Nachteile anderer iterativer Verfahren (Jacobi-Methode und Successive Over-Relaxation-Methode) werden diskutiert und umgesetzt.
In the final part of the lecture, numerical concepts for partial differential equations are introduced. The 2D and 3D Poisson's equation is an elliptic PDE which represents the relation between electric potential and space charge density. For given boundary conditions and existing charge density distribution, the potential can be determined numerically in different ways. The Gauss-Seidel method is an iterative approach that approximates the spatially resolved potential in a linear system of equations. Advantages and disadvantages of other iterative methods (Jacobi method and Successive Over-Relaxation method) are discussed and implemented.
Diffusionsgleichung
Diffusion Equation
Eine weitere partielle Differentialgleichung ist die Diffusions- oder Wärmeleitungsgleichung, die den Zusammenhang zwischen der räumlichen und der zeitlichen Änderung der Temperatur eines Mediums beschreibt. Für diese parabolische DGL werden zusätzliche numerische Methoden aus der Familie der Finite-Differenzen-Methoden eingeführt. Die bekannteste Methode ist die Crank-Nicolson-Methode, die ohne weitere Bedingungen numerisch stabil ist.
Another partial differential equation is the diffusion or heat equation, which describes the relationship between the spatial and the temporal change of the temperature of a medium. For this parabolic PDE, additional numerical methods from the family of finite afference methods are introduced. The most well-known method is the Crank-Nicolson method, which is numerically unconditionally stable.
Warum Python?
Why Python
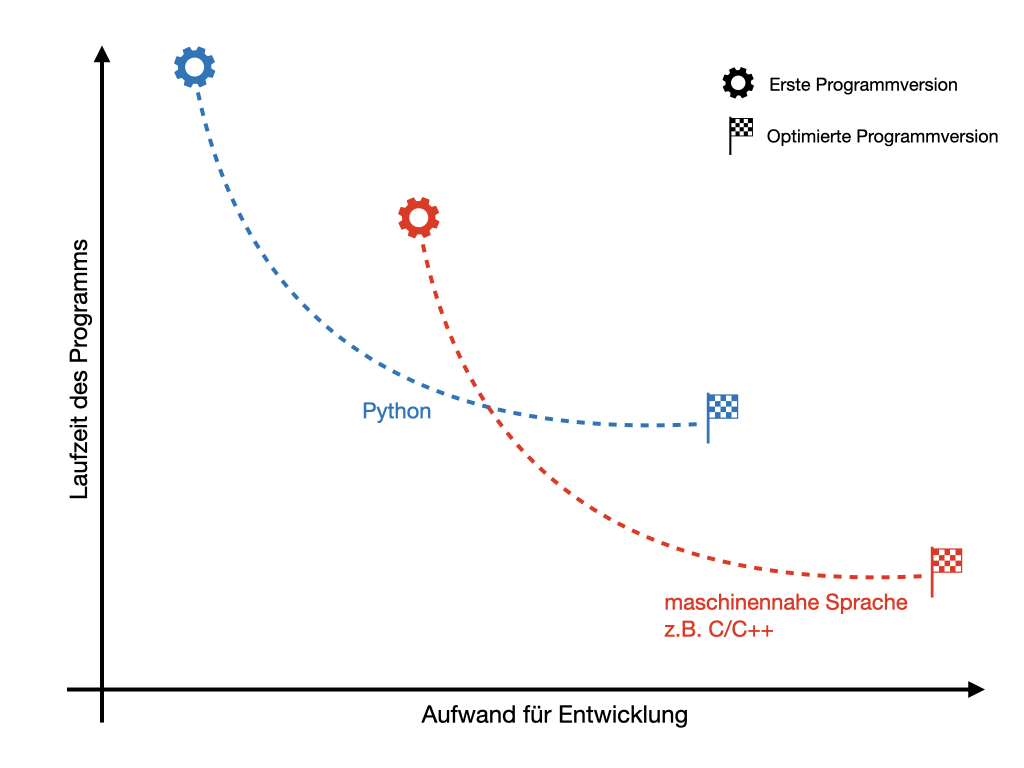
Python ist eine höhere und interpretierte Programmiersprache. Im Gegensatz zu maschinennahen Sprachen wie C/C++ verfügt Python über eine große Auswahl von Bibliotheken, die die Lösung komplexer Probleme (z.B. die numerische Lösung einer Differentialgleichung oder Matrixoperationen) erheblich erleichtern. Ein weiterer Vorteil ist die viel einfacher zu verstehende und zu implementierende Syntax von Python im Vergleich zu vielen anderen Programmiersprachen (keine Deklaration von Variablen). Der interessanteste Vorteil von Python ist aus meiner Sicht die kurze Entwicklungszeit für eine erste lauffähige Programmversion. So kann der Programmcode nach einer Optimierungsphase immer noch abschließend in eine maschinennahe Sprache übersetzt werden, um ggf. die Laufzeit zu verbessern (Nachteil von Python).
Python is a high-level and interpreted programming language. In contrast to machine-oriented languages such as C/C++, Python has a large set of libraries that make it much easier to solve complex problems (e.g. numerical solution of a differential equation or matrix operations). Another advantage is the much easier to understand and implement syntax of Python compared to many other programming languages (no declaration of variables). The most interesting advantage of Python from my point of view is the short development time for a first executable program version. Thus, after an optimization phase, the program code can still be finally translated into a machine-oriented language to improve the runtime if necessary (disadvantage of Python).
Was brauchen wir?
What do we need?

Für die Installation von Python wird eine Distribution wie Anaconda empfohlen. Diese enthält verschiedene Entwicklungsumgebungen wie Spyder oder Visual Studio Code, den Kommandozeileninterpreter IPython und die Webanwendung Jupyter Notebook. Neben der passenden Entwicklungsumgebung ist bei den meisten Python-Distributionen eine große Auswahl an Bibliotheken vorinstalliert, wie NumPy (Vektoren und Matrizen), SciPy (wissenschaftliches Rechnen), Matplotlib (visuelle Darstellungen), Pandas (Verwaltung und Analyse von Daten) und Scikit-learn (maschinelles Lernen). Weitere Programmbibliotheken können in der Regel problemlos nachinstalliert werden. In der Vorlesung "Numerische Methoden in der Elektrodynamik" liegt der Fokus auf den Bibliotheken NumPy und Matplotlib.
For the installation of Python, a distribution such as Anaconda is recommended. This contains various development environments such as Spyder or Visual Studio Code, the command line interpreter IPython and the web application Jupyter Notebook. In addition to the appropriate development environment, most Python distributions have a large selection of libraries pre-installed, such as NumPy (vectors and matrices), SciPy (scientific computing), Matplotlib (visual representations), Pandas (management and analysis of data) and Scikit-learn (machine learning). Further program libraries can usually be installed later without any problems. In the lecture "Numerical Methods in Electrodynamics" the focus is on the libraries NumPy and Matplotlib.